Chapter 1 Timothy Teng

Factor
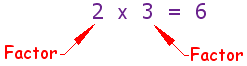
Factors are numbers you can multiply together to get another number: Example: 2 and 3 are factors of 6, because 2 × 3 = 6.

Multiple

more ...

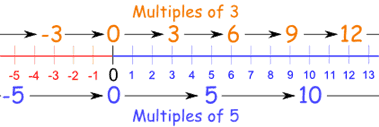
The result of multiplying a number by an integer (not a fraction). Examples: 12 is a multiple of 3, because 3 × 4 = 12 -6 is a multiple of 3, because 3 × -2 = -6 But 7 is NOT a multiple of 3  Index Notation (Note: Index and Power mean the same things as Exponent) The exponent (or index or power) of a number says how many times to use the number in a multiplication. 102 means 10 × 10 = 100 (It says 10 is used 2 times in the multiplication) Example: 103 = 10 × 10 × 10 = 1,000 In words: 103 could be called "10 to the third power", "10 to the power 3" or simply "10 cubed" Example: 104 = 10 × 10 × 10 × 10 = 10,000 In words: 104 could be called "10 to the fourth power", "10 to the power 4" or "10 to the 4"

Prime Factorization

"Prime Factorization" is finding which prime numbers multiply together to make the original number.

Here are some examples:

Example 1: What are the prime factors of 12 ?

It is best to start working from the smallest prime number, which is 2, so let's check:

12 ÷ 2 = 6

Yes, it divided evenly by 2. We have taken the first step!

But 6 is not a prime number, so we need to go further. Let's try 2 again:

6 ÷ 2 = 3

Yes, that worked also. And 3 is a prime number, so we have the answer:

12 = 2 × 2 × 3

As you can see, every factor is a prime number, so the answer must be right.

Note: 12 = 2 × 2 × 3 can also be written using exponents as 12 = 2² × 3