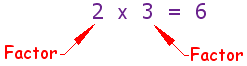Number Line

by Mr Johari

Some conventions that need to be remembered when graphing on a number line are explained below.

1.  An open circle is placed on the number line to show that the number denoted at the circle is not included in the solution set.

2.  A circle that is filled in is placed on the number line to show that the number denoted at the circle is included in the solution set.

3.  Draw arrow on the left only.

4.  For a range of values:
     example    Graph: x < 4

   Solution: The problem asks you to graph all numbers
             that are less than 4.
    

Number Line - Chelsea, Xue Qin, Kimberly, Timothy, Taufiq, Khairul

Number Line

Square root of -1: Not a rational or irrational number, not a positive or negative number, not even or odd.

Negative 2 whole 8 over 11: It is not a cube root, cannot be square rooted it has unending decimals and it is not a rational nor irrational number.

0.23: Not a prime, not a composite, cannot be square rooted, cannot be cube rooted, positive number.

2 whole 3 over 7 : a mixed number, unending decimal, real number and is positive.

Square root of 17, cannot be square rooted, is not a rational number, is a real number and is positive.

22/7 is a rational number and is a mixed number.

                                       

Number line by Eunice, Nehal, Kai Cheng, Hong Yi, Sean and Kenric

This is our number line

Number Line (Chester, Beverly, Luke, Ryan & Bryan Goh

φ (Phi)

The 21st number of the Greek alphabet

The golden ratio  in mathematics, art, and architecture.

4

positive number

smallest composite number

whole number 

even number

13

prime number

positive number

whole number 

odd number

27

composite number

sum of two perfect squares(25 and 2)

whole number 

odd number

perfect cube

positive number

real number

composite number

NUMBER LINE

by Mr Johari

Source: mathsnacks.org and number line addition by Peter Weatherall

Whole numbers are no better than any others! Practice plotting values on the number line as a passionate activist rises up and demands equity for all numbers, including fractions and decimals. Number Rights addresses number and operations standards as well as the process standard, as established by the National Council of Teachers of Mathematics (NCTM). It supports students in: Comparing and ordering fractions, decimals, and percents efficiently and finding their approximate locations on a number line. Building new mathematical knowledge through problem solving. Solving problems that arise in mathematics and in other contexts. View the Downloads page for all Math Snacks.

DECIMALS & FRACTIONS ON THE NUMBER LINE

ADDITION ON THE NUMBER LINE

Other Links

http://mathsnacks.com/numberRights.html

NUMBER LINE

by MR JOHARI

TASK 1

Answer the following questions and post as a Blog entry.

1. What is a Number Line and what stories does it tell?
2. How different is this from the Number system that you have created earlier?

ADDITION AND SUBTRACTION

=======================================================================

TASK 2

1.   Each student will be given a number by the teacher. 

      DO NOT disclose your number.

2.   Find information about the number to describe it better without its identity.

      You may use your LD to search for information where necessary.

      example:   1    is a whole number, it is also an integer,  it is a factor of other numbers.

3.   The teacher will then task you to arrange the members of your group according to their position in 

      the number line. DO NOT disclose your number. Use the descriptors to arrange members in the  

      number line.  eg. if given -3,  0.5,  0 , 8 1/2  then the arrangement would be 

                                              -3,  0,    0.5,  3/4 , 8 1/2

4.   As a group indicate the position of everyone on the number line. It should be a SOLID DOT on the 

      line

Number System (Yu Hin, Bryan Lee)

Number System (Beverly, Timothy, Bryan Goh)

Please click on the picture to view the words.

number system mindmap. (Khairul, Taufiq)

Number Tree (Sean, Qayyum, Kimberly)

Number system ( Lynette , Ryan ,Luke)

6 AM Quiz: Bridge Crossing

---

The 6 AM Quiz is a platform to engage those who would like to seek deeper exploration and understanding of selected topics. It is therefore not compulsory.

---

Solve your puzzle and present the possible solution in the Comments
While you tried to solve the puzzle, what mathematical knowledge and skills did you apply to solve the problem?

ACE LEARNING MATHS PORTAL

BY MR JOHARI

ACE LEARNING is a Mathematics Portal for on-line teaching and Learning in SST.

Objectives:

• a platform for teaching and learning that could be used pervasively and effectively by teacher and students. This includes teaching resources, assessment resources and communication platforms
• develop Learner self independence in learning through the various available on-line resources provided by the portal

URL:  http://www.ace-learning.com/index.php

For first time User: 

Username: NRIC 

Password:  NRIC

You may change your Password after the first Login.

[Please inform your Maths Teacher should you encounter any problem]

                                

Task: Compulsory

Follow the following instructions:

1.  Login to ACE Learning Maths Portal. URL:  http://www.ace-learning.com/index.php

2.  Under the heading Subject; Go to Sec 1 Express

     Click Arithmetic: Factors and Multiples 

     [you will notice a whole array of topics appearing as shown below]

3.   Click Squares, Square Roots, Cubes and Cube Roots and you will notice and screen below.

4.   Go through the lesson on your own (use a headphone so as not to distract others, otherwise lower the volume) Go through all the Examples (you may fast forward the process if you have understood the concepts fully)

5.  Once you are confident of the Topic attempt the following On-line Quiz.

SQUARE AND SQUARE ROOT - COLLABORATION

by Mr Johari Activity 1:

What is a Square?
What are its properties?
Is your perspective of a square necessary to be the same as your friends? why?

CLICK HERE to post your findings.

Math booklet Q4 (Sean, Nehal and Eunice)

Math Booklet Q9: Beverly

Math Booklet Q5 (Kai Cheng, Kenric, Hong Yi)

HCF & LCM Q10

So once you find the LCM of all the numbers,you should get :
2 x 7 x 3 x 2 x 3 x 5 x73= 91980
But 91980 is in days, so in years you should have:91980 divided by 365(1 year on Earth) so you         should get 252 years.
So the next year that an eclipse would occur on Earth would be in the year :1992 + 252 = 2244
So the answer is :2244

Math booklet Q8: Myat Noe, Lynette and Sabrina

Math Booklet Q7: Timothy, Taufiq and Kharui

Add caption

Question 7: 1.20 p.m.

Math Booklet: Aliff, Yu Hin and Bryan Lee

Find the HCF and LCM of 54, 90 and 180

HCF= 18

LCM= 540

Math Booklet (Chelsea Seah, Ee Xue Qin, Kimberly Tan)

Question 6:

NUMBER SYSTEM (3)

by Mr Johari

____________________________________________________________________________

The table above shows 2 categories of numbers as depicted by the blue and white shadings. identify these categories of numbers and give 2 additional examples each per category.

_____________________________________________________________________________

post your responses as a 'comment'

NUMBER SYSTEM (1)

by Mr Johari

Every picture paints a thousand words.

____________________________________________________________________________

The table above shows a numeral models of various civilizations. What is/are the message(s) that the table tries to communicate to us?

_____________________________________________________________________________

post your responses as a 'comment'

Chapter 1 : Sean and Hong Yi

DEFINITIONS:

MULTIPLE: The result of multiplying a multiple by an integer(not a fraction)

               http://www.mathsisfun.com/definitions/multiple.html

                      

FACTOR:Factors are numbers you can multiply together to get another number
           http://www.mathsisfun.com/definitions/factor.html

             

INDEX NOTATION : The exponent (or index or power) of a number says
                              how many times to use the number in a multiplication

http://www.mathsisfun.com/index-notation-powers.html

                              

PRIME FACTORISATION : "Prime Factorization" is finding which prime numbers multiply together to make the original number.
                                 http://www.mathsisfun.com/prime-factorization.html

NUMBER SYSTEM (2)

by Mr Johari

The world of numbers is certainly mind boggling as demonstrated by the clip 'Donald in Mathmagic Land' 

____________________________________________________________________________

_____________________________________________________________________________

The diagram above shows different categories of numbers in the number system.

Please find (1) the definition and (2) a few examples of that categories of numbers.

example:

Whole Number : (1) Also called counting number. one of the positive integers or zero; 

                      (2) {0, 1, 2, 3,…}.

source: http://dictionary.reference.com/browse/whole+number

_____________________________________________________________________________

post your responses as a 'comment'

Chapter 1: (Yu Hin, Qayyum, Bryan lee)

DEFINITIONS:

MULTIPLE 
The result of multiplying a number by an integer (not a fraction).

Examples: 
12 is a multiple of 3, because 3 × 4 = 12
-6 is a multiple of 3, because 3 × -2 = -6
But 7 is NOT a multiple of 3 

INDEX NOTATION














PRIME FACTORISATION
"Prime Factorisation" is finding which prime numbers multiply together to make the original number.

"Factors" are the numbers you multiply together to get another number:

Chapter 1 (Qayyum)

Definitions:

Multiples: Multiples are numbers that are divisible by a certain number without any remainder.
eg. 8/2=4
Since there is no remainder 8 is a multiple of 2.

Prime factorisation: is multiplying prime numbers only to get the original number.
eg. 28=7*4
but 4 is not a prime so have to break it down further
28=7*2*2

Index notation:Is to simplify an equation that includes squaring or cubing etc. etc.........

eg. instead of writing 
2*2*2
one can simply write what is in the above diagram.

Chapter 1 Timothy Teng

Factor
Factors are numbers you can multiply together to get another number: Example: 2 and 3 are factors of 6, because 2 × 3 = 6.

Multiple

more ...

The result of multiplying a number by an integer (not a fraction). Examples: 12 is a multiple of 3, because 3 × 4 = 12 -6 is a multiple of 3, because 3 × -2 = -6 But 7 is NOT a multiple of 3  Index Notation (Note: Index and Power mean the same things as Exponent) The exponent (or index or power) of a number says how many times to use the number in a multiplication. 102 means 10 × 10 = 100 (It says 10 is used 2 times in the multiplication) Example: 103 = 10 × 10 × 10 = 1,000 In words: 103 could be called "10 to the third power", "10 to the power 3" or simply "10 cubed" Example: 104 = 10 × 10 × 10 × 10 = 10,000 In words: 104 could be called "10 to the fourth power", "10 to the power 4" or "10 to the 4"

Prime Factorization

"Prime Factorization" is finding which prime numbers multiply together to make the original number.

Here are some examples:

Example 1: What are the prime factors of 12 ?

It is best to start working from the smallest prime number, which is 2, so let's check:

12 ÷ 2 = 6

Yes, it divided evenly by 2. We have taken the first step!

But 6 is not a prime number, so we need to go further. Let's try 2 again:

6 ÷ 2 = 3

Yes, that worked also. And 3 is a prime number, so we have the answer:

12 = 2 × 2 × 3

As you can see, every factor is a prime number, so the answer must be right.

Note: 12 = 2 × 2 × 3 can also be written using exponents as 12 = 2² × 3

Chapter1: Nehal Janakraj, Eunice Koo

DEFINITION:

FACTORS:

Factors are numbers you can multiply together to get another number:
Example:
2 and 3 are factors of 6, because 2X3=6


MULTIPLES:

The result of multiplying a number by an integer(not a fraction)
Example:
12 is a multiple of 3, because 3X4=12


PRIME FACTORISATION:
"Prime Factorisation" is finding which prime numbers multiply together to make the original number.


INDEX NOTATION:

The exponent (or index or power) of a number says how many times to use the number in a multiplication

example:

10² means 10 × 10 = 100

Chapter 1 (Chester, Xue Qin, Kenric)

DEFINITION:

PRIME FACTORISATION

 MULTIPLE

            FACTOR

Chapter 1: Luke, Ryan, Kai Cheng

DEFINITION

MULTIPLE:

FACTOR:

INDEX NOTATION:

PRIME FACTORISATION:

SOURCE: http://www.mathsisfun.com